Teoria

Rotazioni nello spazio $\mathbb{E}^3$ descritte tramite trasformazioni affini

Una rotazione può essere descritta tramite una trasformazione affine $ \alpha \begin{cases} A \\ \underline{c} \end{cases} $ in un sistema di riferimento ortonormale $\mathcal{R}=\{O,<\underline{e_1},\underline{e_2},\underline{e_3}>\}$ usando una matrice $A$ quadrata $3\times3$ ortogonale speciale e un vettore $\underline{c}$.

Di seguito viene spiegato come eseguire rotazioni tramite gli angoli di Eulero, nell’assunzione che l’origine $O$ di $\mathcal{R}$ coincida col centro dell’oggetto da ruotare.

Angoli di Eulero

Per rappresentare le rotazioni, viene utilizzata una cosiddetta matrice ortogonale speciale $A \in SO(3)$.

Una matrice ortogonale speciale $SO(3)$ è una matrice ortogonale in cui si ha determinante pari ad uno, e in cui il prodotto tra la matrice e la sua trasposta è uguale alla matrice identità.

Il vettore $\underline{c}$ invece ha tutti i valori pari a zero, poiché non vengono eseguite traslazioni.

Per ruotare usando gli angoli di Eulero, si hanno a disposizione tre assi: $X$, $Y$ e $Z$ e si deve decidere con che ordine applicare le rotazioni.

Il legame tra il verso dell’asse ed il verso della rotazione segue la regola della mano destra.

Per ruotare intorno all’asse $X$ di un angolo $\alpha$: $$ \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\alpha & -sin\alpha\\ 0 & sin\alpha & cos\alpha \end{bmatrix}. $$

Per ruotare intorno all’asse $Y$ di un angolo $\beta$: $$ \begin{bmatrix} cos\beta & 0 & sin\beta\\ 0 & 1 & 0\\ -sin\beta & 0 & cos\beta \end{bmatrix}. $$

Per ruotare intorno all’asse $Z$ di un angolo $\gamma$: $$ \begin{bmatrix} cos\gamma & -sin\gamma & 0\\ sin\gamma & cos\gamma & 0\\ 0 & 0 & 1 \end{bmatrix}. $$

Una generica rotazione $R$ può quindi essere rappresentata moltiplicando le tre matrici nell’ordine scelto. Ad esempio, se si vuole prima ruotare attorno all’asse $Z$, poi all’asse $Y$ ed infine intorno all’asse $X$, la rotazione risultante sarà: $R=R_XR_YR_Z$.

Utilizzando questo metodo tuttavia potrebbe capitare un blocco cardanico (gimbal lock), che verrà descritto di seguito.

Gimbal Lock

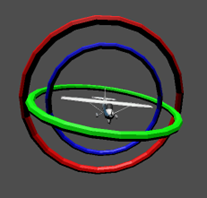
Questa problematica avviene quando due assi di rotazione vengono allineati tra di loro, andando così a perdere un grado di libertà, il che significa che in questa situazione si può ruotare soltanto intorno a due assi e non più intorno a tre. Nell’esempio sulla destra, ruotando intorno all’asse $Y$, si sono allineati gli assi $X$ e $Z$, andando così a creare il problema di cui sopra.

Per poter tornare ad usare tre assi di rotazione, va prima risolto il gimbal lock, disallinenando gli assi (ovvero in questo caso, cambiando la rotazione intorno all’asse $Y$).

Viene di seguito presentato un modo diverso di descrivere rotazioni che non presenta questa situazione problematica.

Quaternioni

Il corpo dei quaternioni $\mathcal{H}$ è formato da elementi di questo tipo: $$q=a+bi+cj+dk$$ con $a,b,c,d \in \mathbb{R}$ e $i^2=j^2=k^2=-1$.

Operazioni sui quaternioni

Dato un quaternione $q=a+bi+cj+dk$ il suo quaternione coniugato è $\overline{q}=a-bi-cj-dk$.

La somma tra quaternioni viene fatta componente per componente (come avviene con i numeri complessi), ed è commutativa.

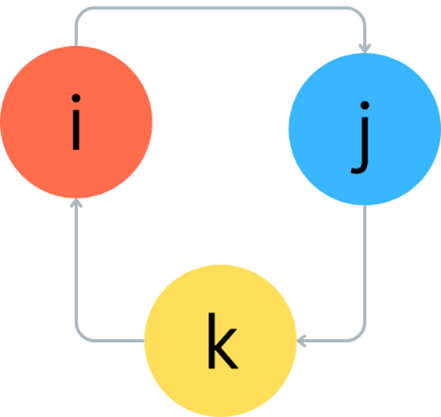
La moltiplicazione invece non è commutativa poiché bisogna tenere a mente le seguenti regole:

$$ki = j, ij = k, jk = i, ik = -j, ji = -k, kj = -i .$$

Inoltre, esiste la norma di un quaternione: $\sqrt{q\overline{q}} = \sqrt{a^2+b^2+c^2+d^2} = \lVert q \rVert \geq 0$ che è un numero reale.

Quaternioni come rotazioni

I quaternioni di norma 1 sono associabili a rotazioni intorno ad una retta passante per l’origine $O$ di $\mathcal{R}$.

Consideriamo un quaternione $q=a+bi+cj+dk$ (diverso da $\pm 1$) e un punto $P \equiv (x, y, z)$ che identifichiamo col quaternione $xi + yj + zk$.

Eseguendo questo calcolo in $\mathcal{H}$:

$$q(xi+yj+zk)\overline{q}$$

si ha come risultato un quaternione $a’+x’i+y’j+z’k$ che corrisponde al punto $P’ \equiv (x’, y’, z’)$ che è il ruotato di $P$ intorno ad una retta $r$, passante per $O$, di direzione data da un versore $\underline{w}$ e di angolo $\theta$ con:

$$ \begin{cases} \underline{w} = \frac{b\underline{e_1}+c\underline{e_2}+d\underline{e_3}}{\lVert b\underline{e_1}+c\underline{e_2}+d\underline{e_3}\rVert} \\ \theta = 2arcos(a) \end{cases}. $$

Bisogna inoltre notare che $\underline{w} = \underline{0}$ solo se $a = \pm 1$ e $b,c,d = 0$.

Data una rotazione intorno ad una retta $r$, sempre passante per $O$, con direzione $\underline{w}$ (un versore) di angolo $\theta$, è possibile trovare un quaternione $q$ che la descrive (ne esistono due, se una possibilità è $q$, l’altra è $-q$) basta considerare:

$$ q = cos \frac{\theta}{2} + sin \frac{\theta}{2} (w_1i + w_2j + w_3k). $$

Esempio di gimbal lock con gli angoli di Eulero

Nel seguente esempio ogni rotazione possibile è espressa da $R = R_XR_YR_Z$.

Noi vogliamo cercare rotazioni di un angolo $\theta$ attorno all’asse $X$; dunque $R$ dovrà avere una forma del tipo:

$$ R = \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta & -sin\theta\\ 0 & sin\theta & cos\theta \end{bmatrix} $$

Partendo da una situazione di gimbal lock, per esempio, $R_X$ ed $R_Z$ potrebbero essere dello stesso tipo, quindi:

$$ R_X = \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\alpha & -sin\alpha\\ 0 & sin\alpha & cos\alpha \end{bmatrix} $$

$$ R_Z = \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\gamma & -sin\gamma\\ 0 & sin\gamma & cos\gamma \end{bmatrix}. $$

Considerando $\alpha = \frac{\pi}{6}$ e $\gamma = \frac{\pi}{3}$ si hanno:

$$ R_X = \begin{bmatrix} 1 & 0 & 0\\ 0 & \frac{\sqrt{3}}{2} & -\frac{1}{2}\\ 0 & \frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} $$

$$ R_Z = \begin{bmatrix} 1 & 0 & 0\\ 0 & \frac{1}{2} & -\frac{\sqrt{3}}{2}\\ 0 & \frac{\sqrt{3}}{2} & \frac{1}{2} \end{bmatrix}. $$

A differenza di $R_X$ e $R_Z$, $R_Y$ non è allineato ed è quindi libero di ruotare intorno all’asse $Y$, di un certo angolo $\beta$:

$$ R_Y = \begin{bmatrix} cos\beta & 0 & sin\beta\\ 0 & 1 & 0\\ -sin\beta & 0 & cos\beta \end{bmatrix}. $$

Ora è quindi possibile calcolare $R$:

$$ R = R_XR_YR_Z = R_X\begin{bmatrix} cos\beta & 0 & sin\beta\\ 0 & 1 & 0\\ -sin\beta & 0 & cos\beta \end{bmatrix}\begin{bmatrix} 1 & 0 & 0\\ 0 & \frac{1}{2} & -\frac{\sqrt{3}}{2}\\ 0 & \frac{\sqrt{3}}{2} & \frac{1}{2} \end{bmatrix} = R_X\begin{bmatrix} cos\beta & \frac{\sqrt{3}}{2}sin\beta & \frac{sin\beta}{2}\\ 0 & \frac{1}{2} & -\frac{\sqrt{3}}{2}\\ -sin\beta & \frac{\sqrt{3}}{2}cos\beta & \frac{cos\beta}{2} \end{bmatrix} = $$

$$ =\begin{bmatrix} 1 & 0 & 0\\ 0 & \frac{\sqrt{3}}{2} & -\frac{1}{2}\\ 0 & \frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} cos\beta & \frac{\sqrt{3}}{2}sin\beta & \frac{sin\beta}{2}\\ 0 & \frac{1}{2} & -\frac{\sqrt{3}}{2}\\ -sin\beta & \frac{\sqrt{3}}{2}cos\beta & \frac{cos\beta}{2} \end{bmatrix} = \begin{bmatrix} cos\beta & \frac{\sqrt{3}}{2}sin\beta & \frac{sin\beta}{2}\\ \frac{sin\beta}{2} & \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4}cos\beta & -\frac{3}{4} - \frac{cos\beta}{4}\\ -\frac{\sqrt{3}}{2}sin\beta & \frac{1}{4} + \frac{3}{4}cos\beta & -\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}cos\beta \end{bmatrix}. $$

Quindi:

$$ \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta & -sin\theta\\ 0 & sin\theta & cos\theta \end{bmatrix} = \begin{bmatrix} cos\beta & \frac{\sqrt{3}}{2}sin\beta & \frac{sin\beta}{2}\\ \frac{sin\beta}{2} & \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4}cos\beta & -\frac{3}{4} - \frac{cos\beta}{4}\\ -\frac{\sqrt{3}}{2}sin\beta & \frac{1}{4} + \frac{3}{4}cos\beta & -\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}cos\beta \end{bmatrix} $$

da cui si può evincere che $cos\beta = 1$ e $sin\beta = 0$, dunque $\beta$ dev’essere per forza pari a $2k\pi$ con $k \in \mathbb{N}$.

Sapendo questo, si può andare a calcolare la matrice $R$:

$$ \begin{bmatrix} cos\beta & \frac{\sqrt{3}}{2}sin\beta & \frac{sin\beta}{2}\\ \frac{sin\beta}{2} & \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4}cos\beta & -\frac{3}{4} - \frac{cos\beta}{4}\\ -\frac{\sqrt{3}}{2}sin\beta & \frac{1}{4} + \frac{3}{4}cos\beta & -\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}cos\beta \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4} & -\frac{3}{4} - \frac{1}{4} \\ 0 & \frac{1}{4} + \frac{3}{4} & -\frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}. $$

Infine, per trovare $\theta$ eguagliamo il risultato trovato all’espressione iniziale di $R$:

$$ \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta & -sin\theta\\ 0 & sin\theta & cos\theta \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}. $$

Quindi $\theta$ deve per forza essere pari a $\frac{\pi}{2}$, quando noi vorremmo poter cambiare $\theta$ a piacimento.

Stesso esempio ma con i quaternioni (in cui non avviene il blocco cardanico)

Vogliamo poter ruotare il sistema di riferimento di un qualsiasi $\theta$ attorno all’asse $X$.

Quindi il versore di rotazione è $\underline{w} \equiv (1, 0, 0)$ e l’angolo di cui ruotare è $\theta$.

Il quaternione che rappresenta la rotazione è quindi

$$ q = cos\frac{\theta}{2} + sin\frac{\theta}{2}(1i+0j+0k) = cos\frac{\theta}{2} + sin\frac{\theta}{2}i $$

ed è possibile utilizzarlo indipendentemente da eventuali allineamenti, rendendo impossibile il blocco cardanico.